АРИФМЕТИКА МУЗЫКИ

АРИФМЕТИКА МУЗЫКИ

«Музыка — это бессознательное упражнение души в арифметике». Так считал немецкий философ, математик и физик Готфрид Лейбниц. Если соотнести эти слова с обилием музыки в наше время, можно смело утверждать, что мы, сами того не осознавая, упражняемся в арифметике каждый день.

Я предлагаю вам хоть полчаса поупражняться сознательно. Если, конечно, вас заинтересуют загадки, которые сейчас будут загаданы. И разумеется, если вы не знаете ответов. /93/

Несколько загадок

Наше ухо очень чувствительно, у нижней границы музыкального диапазона оно замечает изменение частоты колебаний всего на один герц, в середине диапазона — на два-три герца, в верхней его части — на пять герц. Другими словами, если частота возрастет, например, с 50 до 51 герца, с 800 до 803 герц, с 3000 до 3005, мы заметим, что звук стал выше. Вспомним, что границы музыкального диапазона простираются от 16 до 4700 герц. Нетрудно подсчитать, что человек в этом диапазоне может различить по высоте около полутора тысяч музыкальных звуков. Естественно предположить, что и в музыке должно использоваться столько же. Между тем их не набирается и сотни. Фортепиано, охватывающее чуть ли не весь диапазон, насчитывает лишь 88 звуков, и это почти все, что мы имеем. Можно добавить несколько самых высоких и самых низких звуков органа, но это не выручает: все равно число используемых в музыке звуков остается в полтора десятка раз меньше того количества, которое наше ухо способно воспринять и различить по высоте.

Такова главная загадка: почему человек выбрал меньше ста звуков из полутора тысяч возможных, а остальные оставил вне музыки вообще?

Не торопитесь отвечать, что трудно, мол, построить фортепиано с таким невероятным количеством клавиш, а если и удалось бы, то играть на нем будет очень сложно. Такое соображение хоть и логично, но не проясняет причину. Есть инструмент, который позволяет музыканту легко взять около четырехсот звуков, отличимых друг от друга по высоте. Это скрипка. На ее грифе нет порожков, и перемещение прижимающего струну пальца на один-два миллиметра уже дает звук другой высоты. Однако скрипач, какие бы сложные пьесы он ни играл в концерте, использует не четыреста, а всего около пятидесяти звуков, даже если выступает один, без сопровождения других инструментов, с которыми надо считаться.

Видите, мы взяли конкретный инструмент, а загадка осталась прежней: почему скрипач использует столь малую долю богатейшего звукового запаса скрипки?

Можно подойти к главной загадке с другой стороны и раздробить ее на несколько мелких. Почему у фортепиано одни клавиши белые, а другие черные? Почему черные располагаются не симметрично, а группами по две и по три? Почему между двумя соседними белыми клавишами кое-где нет черной? Почему звуки, извлекаемые белыми клавишами, имеют собственные названия, а те, что берутся черными, не имеют? Почему с каждой восьмой белой клавиши отсчет названий повторяется?

Вот какой ворох «почему»!

Элементарная арифметика даст нам ответы на заданные вопросы. А чтобы не получать эти ответы готовыми, придется /94/ рассмотреть краткую историю тех звуков, из которых человек построил все грандиозное здание музыки. Во имя ясности мы вынуждены будем что-то упрощать, а что-то смещать во времени, но эти вольности не коснутся сути.

Кое-что о каркасе

Возьмем число сто. Не сто каких-то предметов, а просто число сто. Его можно выразить и по-другому: десять десятков. Если для наглядности мы положим перед собой метровую линейку, то увидим, что десятки обозначены более длинными черточками. Это как бы каркас, в котором размещаются черточки поменьше — единицы.

Для чего мы вспомнили сведения, знакомые нам еще с первого класса? Чтобы сравнить с музыкальным звукорядом. То количество звуков, которыми мы располагаем в музыке, тоже имеет свой каркас — делится на октавы.

В арифметической сотне каждое круглое число завершает предыдущий десяток и служит точкой отсчета для нового. А в музыкальном звукоряде каждый восьмой звук (если не считать пока те, которые берутся черными клавишами) завершает одну октаву и открывает следующую. Отсюда и значение слова «октава» — восьмой.

В арифметике счет десятками имеет известное всем объяснение: он произошел от десяти пальцев на руках. Музыкальная октава тоже имеет природное происхождение, в основе которого лежит слух человека. Как пальцы определили границы десятков, так наше ухо определило границы октав.

Вот как это получилось.

Допустим, мы слышим звук с какой-то определенной частотой. Если вслед за ним мы услышим звук с частотой ровно вдвое больше, то он покажется нам хоть и выше предыдущего, но очень похожим на него по восприятию. Ухо, сравнивая эти два звука, наделяет их одним качеством. Причем они настолько близки по характеру, что, если взять их одновременно, мы услышим не два звука, а один. Естественно, не имело смысла давать разные названия столь похожим звукам, поэтому с каждым удвоением частоты название повторяется. Например, звуки с частотами 55, 110, 220, 440, 880, 1760, 3520 герц называются ля. В каких бы комбинациях мы ни брали одновременно две, три, четыре из этих частот или хоть все вместе, в любом случае мы будем слышать один звук, а не сочетание разных звуков. Не удивительно, что все они имеют одно название.

Но суть, конечно, не столько в названиях, сколько в том, что каждая из этих частот совершенно естественно, сообразуясь с нашим слухом, завершает одну октаву и открывает другую. Названия как раз условны (нынешние, например, появились только в середине нашей эры), как условно и то, с какой ноты /95/ считать начало октавы. Если мы построим такой же ряд частот для ре или ми, числа получатся другими, но все равно каждая следующая частота будет удваиваться, завершая одну октаву и открывая другую. Сейчас началом каждой октавы принято считать звук до, а когда-то считался звук ля, и в буквенном обозначении нот это сохранилось до сих пор: ля выражается латинской буквой А, потом идут В, С и так далее. От старого исчисления сохранилась и эталонная нота: за основу берется звук ля первой октавы, частота которого на всех инструментах должна быть равна 440 герцам.

Вы заметили, конечно, некоторую неясность. Частота 440 герц лежит в середине построенного нами ряда, а мы почему-то приписали ее первой октаве. Дело в том, что первой октавой в музыкальном звукоряде считается самая употребительная, самая ходовая, что ли. На клавиатуре фортепиано она размещается посередине. Правее идут вторая, третья, четвертая и кусочек пятой. Левее — малая октава, большая октава, контроктава и кусочек субконтроктавы.

Вернемся к нашему хоть и грубому, но наглядному сравнению с метровой линейкой. Каждый дециметр состоит из десяти сантиметров, и если мы назовем, например, пятерку, находящуюся в третьем десятке, сразу станет ясно, что имеется в виду число двадцать пять. А если назвать ля третьей октавы, то сразу же можно найти на клавиатуре фортепиано единственный звук из восьми с таким же названием.

Отсюда вытекает следующий вопрос. Ясно, что десять единиц внутри десятка — вещь совершенно естественная, как и десять пальцев на руках. А вот откуда внутри октавы семь нот, а не десять, не пятьдесят, не сто? Внутри второй октавы, например, мы могли бы различить по высоте даже полтораста звуков. Но их всего семь, как и в любой другой, если игнорировать пока пять дополнительных, до которых мы дойдем в свое время.

Оказывается, для музыки семь звуков внутри октавы такая же естественная вещь, как десять пальцев на руках для арифметики. Уже тетива самого первого лука, колеблясь после выстрела, давала готовым тот набор музыкальных звуков, которыми мы почти без изменения пользуемся до сих пор.

Подарок природы

С точки зрения физики тетива и струна — одно и то же. Да и сделал человек струну, обратив внимание на свойства тетивы. А мы уже знаем, что звучащая струна колеблется не только целиком, но одновременно и половинками, третями, четвертями и так далее. Подойдем теперь к этому явлению с арифметической стороны. Половинки колеблются вдвое чаще, чем целая струна, трети — втрое, четверти — вчетверо. Словом, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота ее колебаний. /96/

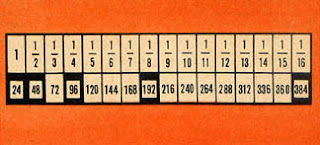
Природный звукоряд. В верхнем ряду показаны доли звучащей струны, а в нижнем — число колебаний, которое дает каждая доля, если целая струна дает 24 колебания в секунду. Квадратиками отмечены удваивающиеся числа, начиная от 24.

Допустим, вся струна колеблется с частотой 24 герца. Высчитывая колебания долей вплоть до шестнадцатых, мы получим ряд чисел, показанных в таблице. Эта последовательность частот так и называется — натуральный, то есть природный, звукоряд.

Начальное число 24 мы выбрали произвольно, чтобы удобнее было считать. При любой другой исходной частоте соотношения получатся одинаковыми, вы можете, если захотите, проверить это. И вообще в музыке важны прежде всего соотношения частот, а не их абсолютные данные, соотношения звуков между собой, а не численные выражения каждого звука. Это легко доказывается: некоторые песни вы наверняка слышали в исполнении и тенора, и баритона, при этом менялись абсолютные частоты звуков, могло измениться и ваше впечатление от разных голосов, но ни на йоту не исказилась мелодия, потому что соотношения ее звуков по высоте остались прежними.

Итак, колеблющаяся струна дала нам природный звукоряд. Вы можете возразить: мол, ни тетиву, ни струну нельзя считать природными телами, потому что их сделал человек. Хорошо, возьмем тогда безусловно природное тело — полый ствол какого-нибудь растения. Мы не можем заставить столб воздуха в стволе колебаться неравными частями. Только целиком, или половинками, или третями и так далее. И если целый столб воздуха колеблется с частотой 24 герца, то половинки дадут 48 герц, трети — 72 и дальше все точно так, как в построенной нами таблице.

С полым стволом растения можно сравнить фанфару, у которой, как мы успели выяснить, нет ни клапанов, ни вентилей, ни боковых отверстий. Играют на ней, следуя только законам природы: заставляют столб воздуха колебаться различными долями. И если /97/ основной тон фанфары мы примем (условно!) за те же 24 герца, следующий будет 48. Музыкант никак не сможет выжать из фанфары звук с частотой между 24 и 48 герцами. Потом пойдет 72, 96 и так далее.

Следовательно, природный звукоряд совершенно одинаков и для тетивы, и для струны, и для пустотелого ствола дерева, и для фанфары.

Присмотримся к нему внимательнее.

Прежде всего определим границы октав, то есть отметим удваивающиеся числа. Это будут частоты, кроме начальной 24, которая служит левой границей, 48, 96, 192, 384. Между 24 и 48 никаких других частот нет. Между 48 и 96 появилась частота 72. Между 96 и 192 — три частоты. А между 192 и 384 — уже полная природная октава, то есть тот звуковой материал, который не нужно было и выбирать — он дан готовым.

Возникает вопрос, с виду вроде бы малосущественный, но по сути очень важный. Почему мы ограничили натуральный звукоряд шестнадцатью элементами? Ведь струна, если иметь в виду идеальное физическое тело, может колебаться бесконечно малыми долями, а не только вплоть до шестнадцатых. Значит, и ряд теоретически можно продолжать бесконечно.

На этот вопрос можно было бы ответить очень просто. Например, так: реальная струна отличается от идеальной тем, что имеет толщину, плотность и предельную длину, поэтому ограничено и число колеблющихся долей. Или так: ни на одном духовом инструменте не удается поделить колеблющийся в нем воздух больше чем на шестнадцать долей.

Но действительный ответ выглядит серьезнее.

Дело в том, что существование натурального звукоряда стало известно гораздо позже, чем оформился определенный строй музыкальных инструментов. Человек, пока еще ничего не зная о подарке природы, интуитивно подстраивал струны между собой так, чтобы они создавали благозвучие. Если инструмент был оснащен грифом, то гриф этот поначалу делался гладким, без порожков, и музыкант просто скользил пальцем по струне как угодно. Но потом он нащупал точки, где звуки получались наиболее естественными, и оснастил эти места грифа порожками. И вот, когда люди открыли природный звукоряд, изучили его и сравнили с тем, что бытовал у музыкантов, оказалось, что полная природная октава, образуемая девятью последними частотами из шестнадцати, почти точно совпадает с октавой, найденной музыкантами самостоятельно. Ухо опередило научные исследования, и получается, что человек, занимаясь музыкой, и в самом деле бессознательно упражнялся в арифметике!

Вы скажете: а при чем здесь подарок, если он был получен с таким опозданием? И будете неправы. Ведь музыкальный слух, который помог интуитивно нащупать естественный звукоряд,— тоже дар природы. /98/

Очень важное «почти»

Мы отметили, что совпадение оказалось почти точным. В чем же заключалась разница?

Взгляните на таблицу, в которой природная октава сравнивается с той, что была выработана человеком. Вы увидите, что музыканты от одной частоты природной октавы отказались совсем, а две частоты чуть-чуть изменили: в нашей таблице вместо 264 стало 256, а вместо 312—320. Вот и все расхождения.

Чем они вызваны?

Музыканты обратили внимание на то, что сочетания некоторых трех звуков между собой воспринимаются особенно естественно и приятно. Потом выяснилось, что это были частоты, относящиеся друг к другу как 4:5:6. В природной октаве есть только одно такое сочетание — в нашем примере это 192:240:288. А музыканты настраивали свои инструменты так, что весь звукоряд превращался в сплошную цепь приятных для слуха трезвучий с соотношением частот 4:5:6.

Чтобы убедиться в этом, выйдем за пределы нашей октавы, добавив справа и слева частоты из соседних октав. Как это сделать, вы уже, наверно, догадываетесь: вправо каждая восьмая частота удваивается, влево каждая восьмая делится на два. Правый конец нашей октавы — восьмой звук от 192. Значит, следующая частота будет восьмой от 216, то есть 432. Левый конец октавы — восьмой звук от 384. Следующий влево будет восьмым от 360, то есть 180. Придерживаясь этого правила, припишем слева еще три частоты. Теперь взгляните на получившуюся таблицу — каждая частота в ней связана с двумя другими частотами соотношением 4:5:6.

Видите, как изменился природный звукоряд от небольших поправок, внесенных человеком! И сколько бы мы ни продолжали

Вверху — природная октава. Внизу — та, что была выработана человеком.

/99/

Музыкальный звукоряд — это сплошная цепь приятных для слуха трезвучий с соотношением частот 4:5:6. В пунктирных клеточках даны частоты из соседних октав.

этот ряд вправо и влево, сколькими бы звуками ни обладал музыкальный инструмент, все они образуют непрерывную последовательность приятных для слуха трезвучий.

Этот ряд, родившийся еще в Древней Греции, в разных странах называется хоть и по-разному, но удивительно схоже: в переводе на русский язык получается «согласие», «порядок», «стройность» и даже «мир». А в самом русском языке такая упорядоченная последовательность звуков называется прекрасным словом «лад».

Задолго до мажора и минора

Чувствую, вы готовы уже высказать некоторое недоумение: книга посвящена музыкальным инструментам, а мы вдаемся в теорию музыки. Потерпите немного, и вы увидите, что все это имеет самое прямое отношение к инструментам.

Взгляните на таблицу, в которой указано отношение каждой последующей частоты к предыдущей. Эти отношения неодинаковы. Если считать девять восьмых и десять девятых целым тоном, то шестнадцать пятнадцатых составят примерно половину целого тона. Значит, к ладу можно присмотреться и с другой стороны — как к чередованию целых тонов и полутонов. Скажем, если взять в качестве начального звука частоту 192, то интервалы выстроятся так: тон, тон, полутон, тон, тон, тон, полутон. А если начать считать с частоты 216, последовательность получится иной: тон, полутон, тон, тон, тон, полутон, тон. С какой бы частоты мы ни начинали отсчет, каждый раз чередование тонов и полутонов будет иным. И тут возникает интересное явление. Лад как соотношение частот един и неизменен. А лад как соотношение целых тонов и полутонов может и изменяться. Если мелодия начинается с частоты 192 — это /100/

Соотношения между соседними частотами неодинаковы. Если 9/8 и 10/9 принять за целый тон, 16/15 составят примерно половину тона.

один лад, с частоты 216 — другой, с частоты 240 — третий и так далее. Каждому такому ладу греки дали свое название. Естественно, их было семь — по числу звуков в октаве. Нам не обязательно приводить здесь эти названия, они есть в любой энциклопедии. Запомним только лидийский лад — в нашем примере он начинался бы с частоты 192.

Уже греки знали, что лад — это не просто формальное чередование тонов и полутонов. Менялся от этого и характер музыки — от нежного, лирического до сурового, мужественного. Во всяком случае, так считали древние музыканты.

Но шло время, и постепенно композиторы все реже и реже стали употреблять греческие лады в их исконном виде. Осталось лишь два основных лада, да и то изменились их названия: теперь мы знаем только мажор и минор. Главное отличие этих ладов таково: у мажора первый полутон идет третьим по счету от начального звука, а у минора — вторым.

Обычно считают, что минор — это обязательно грустный лад, а мажор — непременно бодрый, радостный. Это не совсем так. Достаточно вспомнить, что развеселое «Яблочко» написано в минорном ладу, а скорбная «Аве, Мария» — в мажорном. Но что характер у мажора и минора разный — это бесспорно.

Однако вернемся к древним грекам и посмотрим, как лад привел музыканта к конфликту со своим инструментом. Конфликту, который не разрешен окончательно до сих пор.

Допустим, играл музыкант мелодию в лидийском ладу, начиная, как и положено, с частоты 192. Но вот ему захотелось сыграть ту же мелодию повыше, начав ее, скажем, с частоты 216. Разумеется, древний музыкант мог не иметь никакого представления о частотах — просто захотелось начать с другой струны, чтобы /101/ получилось повыше. В лидийском ладу полутон должен идти третьим по счету, он и шел третьим, пока мелодия начиналась с частоты 192. А теперь, когда ее начали повыше, на инструменте в этом месте никакого полутона не оказалось. Третьим шел целый тон.

Досадно, правда? Семи струн в октаве хватает для исполнения любой мелодии, но при этом не с каждой струны можно ее начать.

Надо было что-то придумывать.

История черных клавиш

Не хотелось бы так часто отсылать вас к таблицам, но что поделаешь — без них в этой теме не обойтись. В очередной таблице определено отношение каждого звука лада к начальному, если этот начальный принять за единицу. Указаны и названия интервалов по отношению к начальному звуку, они же определяют место каждого звука в октаве. Пусть вас не пугают незнакомые термины, они переводятся и запоминаются легко: «прима» — первый, «секунда» — второй, «терция» — третий, и так вплоть до октавы, которая, как мы уже знаем, означает «восьмой». Повторю, что лад — это прежде всего соотношения, а не сами частоты. В других октавах частоты иные, но соотношения остаются теми же. Квинта, например, всегда будет составлять три вторых от примы, то есть от начального звука, терция — всегда пять четвертых, кварта — всегда четыре третьих, октава — всегда ровно два.

Теперь арифметически проанализируем неудачную попытку древнего музыканта начать лидийскую мелодию с другой струны. Естественно, ему нужно было сохранить соотношения. Возьмем в качестве основного звука частоту 216 и выстроим звуки согласно

Отношение каждой частоты к начальной, если начальную принять за единицу. Здесь же указаны названия интервалов.

/102/

Если взять в качестве начального звука мелодии частоту 216, а не 192 и сохранить прежние соотношения, понадобятся новые звуки, которыми инструмент пока не располагает.

тем же соотношениям, которые получались от частоты 192. Это сделано в следующей таблице. Мы увидим, что в пределах нашей октавы появились четыре новых частоты. Инструменту с гладким грифом это не страшно: можно зажимать струны в любом месте и тем самым сохранить нужные соотношения. А инструменту наподобие арфы, в котором каждый звук издается отдельной струной? Нужно добавлять новые струны.

Это еще полбеды — четыре новых струны. Но музыкант хотел бы иметь возможность начинать мелодию в любом ладу с любого звука октавы. И он стал прибавлять новые струны на своем

В тех местах, где интервалы составляли целый тон, древние греки добавили вспомогательные звуки. Вот откуда происходит форма клавиатуры фортепиано.

/103/

инструменте, дошел до двух с лишним десятков в каждой октаве и остановился, здраво рассудив, что таким путем задачу не разрешить. Сейчас подсчитано, что, если бы древний грек последовательно дошел до конца, ему нужно было бы иметь в каждой октаве восемьдесят пять струн. Может быть, ценой невероятных усилий он и научился бы играть на таком инструменте, но уж очень это казалось обидным: мелодии хватает семи звуков в октаве, а все остальные нужны лишь для того, чтобы можно было начинать любую мелодию с любой струны.

И древние музыканты нашли компромиссное решение. Они добавили новые звуки только там, где интервал между основными звуками равнялся целому тону. Не разделили целые тона пополам, нет, ведь это неделимые элементы лада, а просто ввели вспомогательные звуки. Вглядитесь в очередную таблицу — не напоминает ли вам расположение новых звуков черные клавиши фортепиано? Так оно и есть. Вот откуда происходит форма клавиатуры — от древних греков, хотя они и понятия еще не имели в то время о клавиатуре вообще и тем более о клавиатуре в том ее виде, в каком она делается на современных инструментах. И до сих пор у этих вынужденно введенных дополнительных звуков нет собственных названий, а именуются они, например, «до-диез», что означает «выше до», или «ми-бемоль», то есть «ниже ми». Причем один и тот же дополнительный звук можно назвать двояко. Если, скажем, он стоит между соль и ля, это и соль-диез, и ля-бемоль.

Выходит, вся эта история с пятью дополнительными звуками в октаве началась только из-за того, что древние музыканты захотели свободнее переходить из тональности в тональность и из лада в лад? Да, только из-за этого. Самому ладу вполне хватает семи звуков в октаве. И если в какой-то местности бытует одна тональность, то есть в основе мелодии всегда лежит один и тот же начальный звук, то инструмент здесь по-прежнему может обходиться семью звуками в октаве, как прекрасно обходятся до сих пор некоторые гармошки, народные духовые и струнные инструменты.

Но добавление пяти звуков, увы, не до конца решило проблему. Соотношения между соседними звуками все равно оставались разными, искусственно введенные полутона не были равны исконным полутонам лада, поэтому не из любой тональности в любую можно было переходить легко и просто.

И тут мы обязаны вспомнить одного выдающегося грека.

Что придумал Пифагор

Все знают, что он был ученым и, в частности, автором знаменитой теоремы. А то, что он был еще и блестящим музыкантом, известно не так широко. Сочетание этих дарований позволило Пифагору первым догадаться о существовании природного звукоряда. Но надо было еще доказать это. Пифагор построил для своих экспериментов полуинструмент, полуприбор — /104/

Формула музыкального строя, выведенная Пифагором.

монохорд. Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы удобнее было зрительно делить струну на части. Множество опытов проделал Пифагор с монохордом и в конце концов описал математически поведение звучащей струны. Опыты Пифагора легли в основу науки, которую мы называем сейчас музыкальной акустикой.

Пифагору принадлежит и математическое объяснение основ гармонии. Следуя собственной теории совершенства малых чисел, он определял суть гармонии так: наиболее естественно воспринимаются ухом частоты, которые находятся между собой в простых числовых соотношениях. Вот откуда и октава 1:2, и трезвучие 4:5:6.

Когда древнегреческие музыканты ввели пять дополнительных звуков и убедились, что проблема все же осталась, Пифагор взялся за решение уже не теоретической, а сугубо практической задачи: как настроить инструмент, чтобы не увеличивать количество звуков в каждой октаве сверх двенадцати и в то же время дать возможность музыкантам свободнее переходить из тональности в тональность и из лада в лад?

Расшифровка формулы Пифагора.

/105/

Внутри октавы наиболее слитно с начальным звуком воспринимается квинта, которая составляет с ним тоже простейшее после октавы соотношение — 3:2. Пифагор решил поэтому взять квинту за основу строя и вывел удивительно красивую формулу — полюбуйтесь ею. Но поскольку внешняя красота пока мало о чем говорит, восстановим расчеты Пифагора. Пусть вас не смущают показатели степени в формуле — все опять же сводится к арифметике.

Обратимся к очередной таблице.

Подставляем вместо единицы частоту 384 — правую границу уже хорошо знакомой нам октавы. Условно обозначаем ее до. Вправо от до квинта, то есть пятый звук, считая только основные, а вместе с дополнительными восьмой, будет соль. Частота его — три вторых от 384, то есть 576. Квинта от соль — ре. Частота три вторых от 576 — 864. И так далее, вплоть до фа-диез.

Влево от до квинта — фа. Частота две трети от 384—255,9. Квинта от фа — си-бемоль. Частота две трети от 255,9—170,6. И так до соль-бемоль.

Мы получили ряд из тринадцати частот. Тринадцати, а не двенадцати, потому что крайние справа и слева частоты принадлежат одному и тому же звуку: фа-диез — то же самое, что соль-бемоль.

Теперь этот ряд частот, который охватывает почти весь музыкальный диапазон, нам предстоит свести в одну октаву, то есть последовательным умножением или делением на два (отчего, как мы знаем, название звука не меняется) уложить в промежуток между 192 и 384. Если какая-то частота после умножения или деления на два не улеглась в границы октавы, нужно еще раз умножить или разделить ее на два.

После этих действий мы получим октаву, к которой пришел Пифагор.

Рассматривая ее основные частоты, вы увидите небольшие расхождения с прежним, идеально чистым строем. Вместо частоты 240 появилась частота 243, вместо 320—324, а 360 превратилось в 364,5.

Эти незначительные изменения произвели революцию в музыкальном строе. Интервалы более или менее выровнялись. Определились точные частоты дополнительных звуков. Музыканты, пользуясь теми же двенадцатью звуками в октаве, получили возможность переходить из тональности в тональность гораздо свободнее. Поэтому Пифагоров строй продержался больше двух тысяч лет.

Прежний конфликт музыканта с инструментом был улажен.

Однако наметился новый.

Обратите внимание на то, что в Пифагоровом строе между фа и соль стоят две частоты. Когда мы последовательным делением на два привели крайнюю правую частоту фа-диез в нашу октаву, /106/

Вверху — уже знакомая нам «чистая» октава. Внизу — октава, к которой пришел Пифагор. Видно, что немного изменились три частоты. Зато настраивать инструменты стало значительно проще. В пунктирных клеточках даны частоты дополнительных звуков. Попутное открытие Пифагора: пониженный звук не равен повышенному предыдущему.

получилось одно число. А когда последовательным умножением на два привели в нашу октаву крайнюю левую частоту си-бемоль, получилось другое. Это было попутное открытие Пифагора: пониженный звук не равен повышенному предыдущему. В нашем примере соль-бемоль не равно фа-диез. Если вы продлите по квинтам формулу Пифагора вправо еще на четыре элемента — до-диез, соль-диез, ре-диез и ля-диез — и самостоятельно проделаете все знакомые уже арифметические операции, то убедитесь, что это открытие справедливо для любого дополнительного звука.

Но чтобы не добавлять новые струны, это противоречие разрешили просто: усреднили две частоты и оставили, как и было, между двумя основными звуками один дополнительный. Усреднение это стало традиционным, так что и сейчас, например, пианист вынужден пользоваться одной черной клавишей там, где, согласно точным акустическим расчетам, их должно быть две. А вот скрипач может по-разному взять соль-бемоль и фа-диез, как и другие повышенные и пониженные звуки. Может взять их по-разному и тромбонист — кулиса его инструмента передвигается совершенно свободно. /107/

Усреднение двух близких частот совершенно незаметно для слушателя с обычным слухом, и не в этом суть нового конфликта. Он выявится, если мы подойдем к расчетам Пифагора с другой стороны.

Когда мы располагали звуки по квинтам, самая левая частота соль-бемоль получилась у нас 33,7, а самая правая частота фа-диез — 4374. Давайте попробуем пройти от первого ко второму октавами, то есть последовательным умножением на два. После семи умножений получим число 4313,6. Как видим, оно существенно расходится с 4374 — на шестьдесят герц. А ведь мы имеем дело с одним и тем же звуком. Выходит, целое число квинт не укладывается в целое число октав. Это расхождение называется Пифагоровой коммой. Комма и привела к конфликту.

О лютнистах эпохи Возрождения шутливо говорили так: если они живут шестьдесят лет, то двадцать из них настраивают свой инструмент. Эта шутка основана на действительном явлении. На грифе лютни первое время не было врезанных намертво порожков, гриф просто перевязывался в определенных местах тонким шнурком или жилами. Эти перевязки и образовывали порожки, которые могли передвигаться по грифу. И вот музыканты, так и этак передвигая порожки, искали наилучшее их расположение, чтобы не так сказывалась Пифагорова комма. Причем это нельзя было сделать раз и навсегда, потому что играли ведь не в одной тональности. Вот и приходилось каждый раз перед концертом приспосабливать лютню к нужным в данном выступлении тональностям.

А настройщики органов, сохраняя чистыми октавы, квинты, а потом и терции, кое-как распределяли Пифагорову комму по другим интервалам, которые от этого получались не совсем чистыми. Музыкант должен был знать заранее, как именно распределена комма и в какой тональности его подстерегают фальшивые звуки. Искусные настройщики умели выходить из положения так. Обычно при игре в двух-трех самых употребительных тональностях некоторые дополнительные звуки, представленные черными клавишами, не используются вообще, остаются как бы в стороне от исполнения. Вот по этим-то звукам и рассовывали комму. Но беда органисту, если он вдруг забудется и возьмет при импровизации какой-нибудь из таких звуков. Тотчас раздается режущая ухо фальшь. Не мудрено, что эти фальшивые звуки были прозваны «волками».

Конечно, музыкантам трудно было смириться с раздражающим неудобством. Особенно досадовали органисты: ведь органу присуща уникальная длительность звука. Одно дело фальшь на лютне, там звук быстро затухает, и совсем другое, когда «волком воет» орган!

Не удивительно поэтому, что именно органист предложил следующую и пока последнюю реформу музыкального строя. Было это в конце семнадцатого века. /108/

Все равны!

Андреас Веркмейстер был не только органистом, но и теоретиком музыки. Он сформулировал задачу так. Первое: нужно сохранить в октаве двенадцать традиционно устоявшихся звуков. Второе: все соотношения между соседними частотами должны быть абсолютно равными. Третье: никакой коммы не должно быть.

Поставленная таким образом задача имеет единственное решение: каждая последующая частота будет относиться к предыдущей так, как корень двенадцатой степени из двух относится к единице.

А если говорить проще, Веркмейстер равномерно распределил Пифагорову комму между всеми звуками внутри каждой октавы. Комма рассосалась, растворилась, стала почти незаметной. Но досталось это дорогой ценой: не осталось ни одного чистого интервала внутри октавы. Веркмейстер не пощадил даже квинту — этот интервал, тысячелетиями считавшийся незыблемым, стал чуть короче. Как вы догадываетесь, ровно на /95/ столько, что теперь двенадцать квинт точно укладывалось в семь октав. Сама октава вышла из этой передряги без потерь — она единственная осталась чистой.

Многих музыкантов поначалу возмутило предложение Веркмейстера. Ни одного чистого интервала внутри октавы — это казалось посягательством на первоосновы музыки. Однако через два-три десятилетия, прислушавшись, почти все смирились с компромиссом, потому что разница между чистой настройкой и той, что предложил Веркмейстер, была едва уловимой, а достоинства нового строя постепенно стали очевидными. Исчезли «волки». Стало возможным переходить из тональности в тональность и из мажора в минор как угодно. В ладу, естественно, остались те же семь основных звуков, но теперь любой лад мог открываться с любой клавиши, хоть с черной. Впервые делом доказал это великий Бах, написав цикл произведений для всех двадцати четырех тональностей — двенадцати минорных и двенадцати мажорных. До реформы Веркмейстера такое количество тональностей существовало лишь теоретически, а на практике было невыполнимо, ибо пришлось бы чуть не для каждой из них заново перестраивать инструмент.

Можно было бы привести еще одну таблицу для математической демонстрации нового строя, но лучше всего представить себе современную музыкальную шкалу, глянув на гриф гитары. Каждое расстояние между порожками относится к соседнему, меньшему, как корень двенадцатой степени из двух относится к единице.

Казалось бы, все хорошо, но проблемы остались до сих пор.

Музыканты с особо тонким слухом чувствуют неточность настройки, их не удовлетворяет отсутствие строгой чистоты звучания многих инструментов. Известно, как мучился композитор Александр Скрябин, не находя в строе рояля чистых квинт, терций /109/ и других интервалов. А русский музыкант и музыкальный критик прошлого века Владимир Одоевский даже заказал себе рояль, в каждой октаве которого было не двенадцать, а семнадцать клавиш. Этот рояль сейчас можно увидеть в московском Музее музыкальной культуры имени Глинки.

Компромиссным остался и строй оркестра. Фортепиано, челеста, ксилофон настраиваются по Веркмейстеру. Вся скрипичная группа может играть в чистом строе, но вынуждена подлаживаться. А медные трубы, у которых нет отверстий в боку, и хотели бы подладиться, да не могут. Ведь труба, гни ее или скручивай, остается трубой, физическим телом, и ни наш слух, ни Пифагор, ни Веркмейстер не в состоянии ничего с ней поделать. До сих пор медные духовые играют в натуральном строе, и композиторы, поручая им ту или иную партию, учитывают те звуки, которые особенно заметно расходятся с нынешним музыкальным строем. Даже настройка гитары, домры, мандолины остается проблемой для музыканта с тонким слухом. Эти и другие инструменты с порожками на грифе, даже если они сделаны мастером безукоризненно, в принципе нельзя настроить абсолютно верно, потому что струны между собой должны настраиваться чисто, а порожки в гриф врезаются по Веркмейстеру. Возьмем, например, классическую гитару. Звук, взятый, скажем, на прижатой к пятому порожку второй струне, не вполне соответствует звучанию открытой первой струны, а между тем это один и тот же звук ми.

Таковы нерешенные проблемы.

А кроме проблем, остались интересные вопросы. Математически все тональности равны, но почему у многих композиторов есть любимые? Почему тональности, даже если все они минорные или все мажорные, кажутся им разными?

Были попытки как-то объяснить это, но удовлетворительных ответов пока нет. Видимо, и здесь вступает в силу то знаменитое «чуть-чуть», которое есть в любом искусстве. И никакая арифметика здесь уже не поможет.

Газарян С.С.

В мире музыкальных инструментов: Кн. Для учащихся ст. классов. – М.: Просвещение, 1985. – С. 93